Gaussian Processes

In progress! Check back again soon!
Today, we’re going to look at Gaussian processes. A lot of the reference material (CS229: Gaussian Processes) is really good, so we’re not going to redo all of the work that they’ve done. Instead, the idea is to look deeper at some of the results derived there.

Review: Random Variables

A random variable \(X\) on \(\Omega\) (called the sample space) is a function \(\Omega \to \mathbb{R}\). We define the cumulative distribution \(F_X: \mathbb{R} \to [0, 1]\) of \(X\) as: \[ F_X(x) = P(X \leq x) = P(w \in \Omega \mid X(w) \leq x) \] If the \(F_X(x)\) follows a particular well-known form, such as that of a normal (Gaussian) random variable \(\mathcal{N}(\mu, \sigma^2)\): \[ F_{\mathcal{N}(\mu, \sigma^2)}(x) = \int_{-\infty}^{x} \frac{e^{-\frac{1}{2}\left(\frac{t - \mu}{\sigma}\right)^2}}{\sqrt{2\pi\sigma^2}} dt \] then, we say that \(X\) is normally distributed with mean \(\mu\) and variance \(\sigma^2\), or: \[ X \sim \mathcal{N}(\mu, \sigma^2). \]

Note that a random variable is completely deterministic: once we fix \(w \in \Omega\), \(X(w)\) is completely determined. Where does randomness come from then? The answer is in our choice of \(w\). Sampling from a random variable requires us to pick \(w\) randomly from \(\Omega\) and pass it through \(X\). If the form of \(X\) is known, the distribution of \(X\) can shed light on how \(w\) is picked, but generally, we care only about the values of \(X(w) = x\) (which is what \(F_X\) tells us about), and not \(w\) itself.

We can collect random variables to get a random vector \(X = [X_1 \ldots X_n]\) which is now a function \(\Omega \to \mathbb{R^n}\). The cumulative distribution function \(F_X\) now maps tuples in \(\mathbb{R}^n\) to probabilities in \([0, 1]\). We can extend the univariate normal distribution to get a multivariate normal distribution, now parametrized by a mean vector \(\mu\) and a covariance matrix \(\Sigma\).

When we talk about a distribution over a set \(S\), we are assigning probabilities to elements (samples from the distribution) in \(S\). Each random variable induces a distribution over \(\mathbb{R}\), while each random vector induces a distribution over \(\mathbb{R}^n\): given by the respective cumulative distribution functions.

Review: Random Functions

The reference above talks about how functions on finite domains \(\mathcal{X}\) can be treated as samples from a random vector of dimension \(\lvert \mathcal{X} \rvert\): index the domain \(\mathcal{X}\), and then, for each \(x \in \mathcal{X}\), assign the value at the corresponding index in the sample.

Suppose, we specify that our functions are sampled from the multivariate normal distribution over \(\mathbb{R}^n\). How does these functions depend on the parameters of the normal distribution? Well, we would expect to see the samples distributed around the mean. Further, the covariance matrix of the distribution tells us how related two dimensions \(d_i\) and \(d_j\) in the random vector samples are. The values of the samples at these dimensions corresponds to the function values \(f(x_i)\) and \(f(x_j)\). It would be nice to have the covariance matrix entry \(\Sigma_{ij}\) depend on \(x_i\) and \(x_j\): this allows us to say that, if \(x_i\) and \(x_j\) are close, so should \(f(x_i)\) and \(f(x_j)\).

Once this makes sense, we can extend this analogy to how functions on infinite domains can be treated as samples from a random process (such as a Gaussian process).

A Gaussian process \(G\) on \(\mathcal{X}\) is defined by two functions: the mean function \(m: \mathcal{X} \to \mathbb{R}\), and the covariance function \(k: \mathcal{X} \times \mathcal{X} \to \mathbb{R}\). We have seen that a valid covariance function is necessarily a kernel. \(G\) assigns Gaussian random variables to elements in \(\mathcal{X}\). In fact, any collection of these Gaussian random variables will have a distribution of a multivariate Gaussian, whose parameters depend on the elements chosen.

If the above seems complicated, think of \(G\) as a collection of random variables \(\{G(x) \mid x \in \mathcal{X}\}\) in a row. The random variable corresponding to \(x \in \mathcal{X}\) is given by \(G(x)\). Now, sampling from \(G\) gives us values in \(\mathbb{R}\) for each of the random variables \(G(x)\). Thus, each sample can be thought of as a function over \(\mathcal{X}\), just as before. The specificities of how the samples are distributed are given by the mean and covariance functions.

The similarity between random variables \(G(x_i)\) and \(G(x_j)\) is explicitly through the kernel \(k\). The kernel gives rise to \(k(x_i, x_j)\), which is the covariance of \(G(x_i)\) and \(G(x_j)\). This is what we were hinting at the end of the second paragraph in this section.

Thus, we now have a way to specify a distribution over functions: we will call functions sampled from such a distribution as ‘random’ functions. Again, random functions are completely deterministic.

An Example

We will consider an example similar to the one in the previous post on functional gradient descent.
Consider the regression problem, where \(x_i,\) for \(i \in {1, \ldots, 200}\) are linearly spaced in \([-1, 1]\): \[ y_i = e^{-\left(\frac{x_i - 0.5}{0.5}\right)^2} + e^{-\left(\frac{x_i + 0.5}{0.5}\right)^2} + \mathcal{N}\left(0, \frac{1}{2000}\right) \]

The form of \(y\) above allows us to set the error variance (\(\sigma^2\) for \(\epsilon\)) as \(\frac{1}{2000}\).

We will use the RBF kernel, as before.

We are adding samples into our training set one at a time. Note that this corresponds to adding a new row and a column to the current kernel matrix \(K(X, X)\), keeping the remaining entries the same. Thus, we do not need to rebuild the entire kernel matrix at each step. Similarly, an addition of a new training sample means adding a row at the bottom of the kernel matrix \(K(X, X^*)\). Also, note that the test set is fixed, and the kernel matrix \(K(X^*, X^*)\) needs to be computed only once.

If we implement all this, and plot the resulting predictive mean with one-sigma error as computed by the predictive variance after the addition of each training sample:

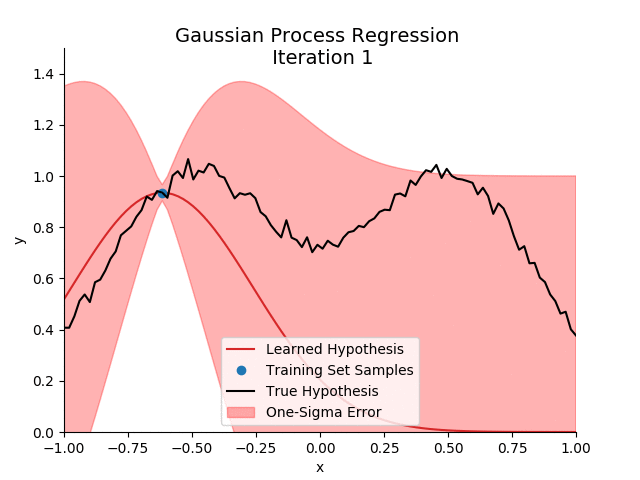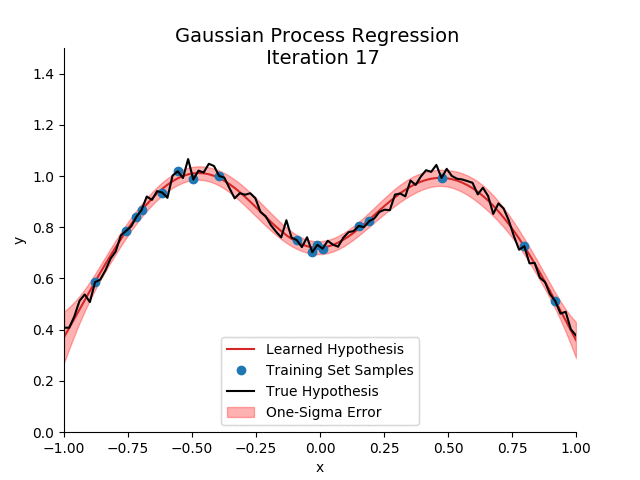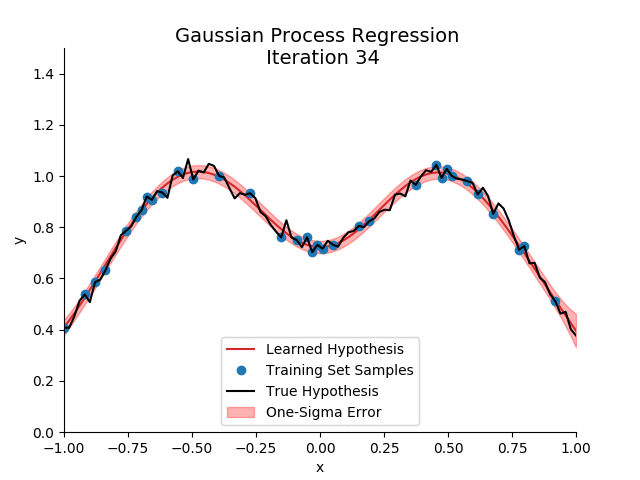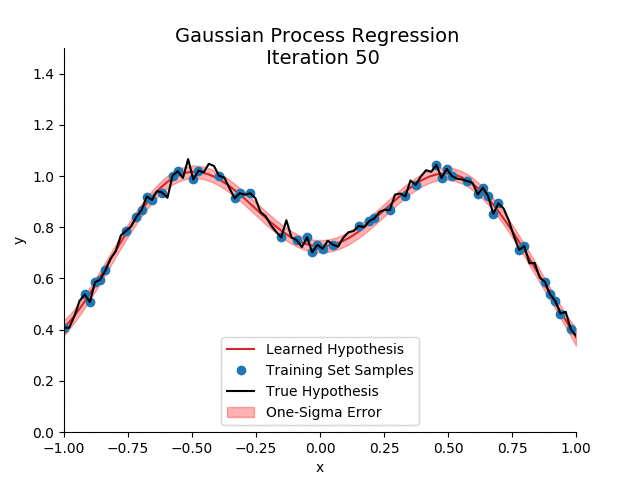
In the example below, I’m actually plotting the predictive distribution over all samples, not just the test set. Note that even at the training samples, the variance is non-zero: capturing the error in \(\epsilon\). More interestingly, initially, there are no training set samples on the right hand side. This leads to a large variance on that subset of the domain, indicated by the wide band of unconfidence. However, as samples from the right hand side enter our training set, the model becomes more confident.

The code for this example is available here.

I’m also starting to introduce a commenting facility via GitHub Issues, in order to not clutter up this space here. Comment here!